Question

Pls

do a step by step i dont understand how to do this hw problem
Find the derivative of the trigonometric function f(x) = 7x cos(-x). Answer 2 Points f'(x) =

Answer 1

`f'(x)=7\cos(-x)+7x\sin(-x)`

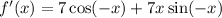
Explanation:

`f(x)=7x\cos(-x)\\f'(x)=(7x)'\cos(-x)+(-1)(7x)(-\sin(-x))\\f'(x)=7\cos(-x)+7x\sin(-x)`

Note by the Product Rule,
`(d)/(dx) f(x)g(x)=f'(x)g(x)+f(x)g'(x)`

Also, by chain rule,
`\cos(-x)=(-x)'(-\sin(-x))=-(-\sin(-x))=\sin(-x)`

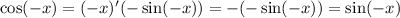
Hopefully you know that the derivative of cos(x) is -sin(x), which is really helpful here.

Hope this was helpful! If it wasn't clear, please comment below and I can clarify anything.