Question

(1 point) Use the divergence theorem to calculate the flux of the vector field F(x, y, z) = x37 + y3] + x3k out of the closed, outward-oriented surface S bounding the solid x2 + y2 < 25, 0 < z< 6. F.

Answer 1

To find the flux of the vector field F(x, y, z) = x3i + y3j + x3k through a closed surface using the divergence theorem, one must first calculate the divergence of F, then integrate this divergence over the volume enclosed by the surface using the appropriate limits and coordinates.

Step-by-step explanation:

The question involves using the divergence theorem to calculate the flux of a vector field F(x, y, z) = x3i + y3j + x3k through a closed surface S. The surface S encloses the solid defined by the cylinder x2 + y2 < 25 within the planes z = 0 and z = 6. The divergence theorem states that the flux of F through S is equal to the triple integral of the divergence of F over the volume enclosed by S.

First, compute the divergence of F:

`/ \mathbf{F} = \\abla \cdot \mathbf{F} = (\partial x^3)/(\partial x) + (\partial y^3)/(\partial y) + (\partial z^3)/(\partial z) = 3x^2 + 3y^2 + 0`

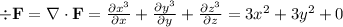
The volume integral of div F over V is:

`\int \int \int_V \text{div} \, \mathbf{F} \, dV = \int \int \int_0^6 \int_0^(2\pi) \int_0^(√(25)) (3r^2) \, r \, d`

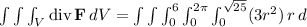
The integral simplifies as we use cylindrical coordinates with r for radius and θ for the angle. After solving, the resulting flux through S is calculated.

Answer 2

The divergence theorem to calculate the flux of a vector field across a closed surface. The divergence of the vector field needs to be computed and integrated over the volume enclosed by the surface.

Step-by-step explanation:

A concept in vector calculus known as the divergence theorem, which is used to calculate the flux of a vector field across a closed surface. To solve this problem, one needs to compute the divergence of the given vector field F(x, y, z) = x3i + y3j + x3k and then integrate this divergence over the volume bounded by the surface S.

To calculate the divergence of F, we take the partial derivative of each component with respect to its corresponding variable:
div F = ∇ · F = ∂(x3)/∂x + ∂(y3)/∂y + ∂(x3)/∂z = 3x2 + 3y2 + 0.

Next, integrate this divergence over the cylindrical volume defined by x2 + y2 < 25 and 0 < z < 6. Since the volume is a cylinder with radius 5 and height 6, we can set up an integral in cylindrical coordinates for simplicity.