Answer:
(a) -
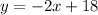
(b) -

Explanation:
Given the equation of a line, which we'll call line 1, find the following.
(a) - The equation of a line, which we'll call line 2, that is parallel to line 1 and travels through the point (9,0)
(b) - The equation of a line, which we'll call line 3, that is perpendicular to line 1 and travels through the point (9,0)
Given:
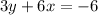
(1) - Write the equation of line 1 in slope-intercept form


Thus, we can conclude the slope of line 1 is -2.
(2) - Answering part (a)
To find a line that is parallel to line 1, the slopes must be the same, -2. Use the point-slope form for a line to find the equation for line 2.
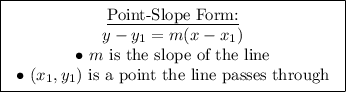

Thus, the equation for line 2 is found.
(2) - Answering part (b)
To find a line that is perpendicular to line 1, the slope of line 3 must be the opposite-reciprocal of line 1's. Once again, use the point-slope form of a line to find the equation of line 3.

Thus, the equation of line 3 is found.