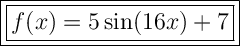Question

Write a sine function with an amplitude of 5, a period of

Pi/8,and a midline at y = 7.

f(x) = 4sin(8x) + 5
f(x) = 5sin(16)+7
f(x) = 5sin(16x) + 4
f(x) = 4sin(8x) + 7

Answer 1

`\textsf{B)} \quad f(x) = 5 \sin (16x) + 7}`

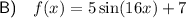
Explanation:

The sine function is periodic, meaning it repeats forever.

Standard form of a sine function

`\boxed{f(x) = A \sin (B(x + C)) + D}`

where:

• A is the amplitude (height from the midline to the peak).
• 2π/B is the period (horizontal distance between consecutive peaks).
• C is the phase shift (horizontal shift - positive is to the left).
• D is the vertical shift (y = D is the midline).

Given values:

• Amplitude, A = 5
• Period, 2π/B = π/8
• Phase shift, C = 0
• Vertical shift, D = 7

Calculate the value of B:

`(2\pi)/(B)=(\pi)/(8)\implies 16\pi=B\pi\implies B=16`

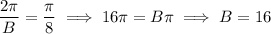
Substitute the values of A, B C and D into the standard formula:

`f(x) = 5 \sin (16(x + 0)) + 7`

`f(x) = 5 \sin (16x) + 7`

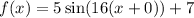
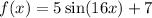
Therefore, the sine function with an amplitude of 5, a period of π/8, and a midline at y = 7 is:

`\Large\boxed{\boxed{f(x) = 5 \sin (16x) + 7}}`