Question

Solve the given initial-value problem. y′′′ 10y′′ 25y′ = 0, y(0) = 0, y′(0) = 1, y′′(0) = −2

Answer 1

`y(t)=(8)/(25) -(8)/(25)e^(-5t)-(3)/(5)te^(-5t)}`

Explanation:

Solve the given initial value problem.

`y''' +10y''+ 25y' = 0; \ y(0) = 0, \ y'(0) = 1, \ y''(0) = -2`

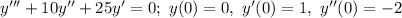
(1) - Form the characteristic equation

`y''' +10y''+ 25y' = 0\\\\\Longrightarrow \boxed{m^3+10m^2+25m=0}`

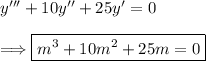
(2) - Solve the characteristic equation for "m"

`m^3+10m^2+25m=0\\\\\Longrightarrow m(m^2+10m+25)=0\\\\\therefore \boxed{m=0}\\\\\Longrightarrow m^2+10m+25=0\\\\\Longrightarrow (m+5)(m+5)=0\\\\\therefore \boxed{m=-5,-5}\\\\\rightarrow m=0,-5,-5`

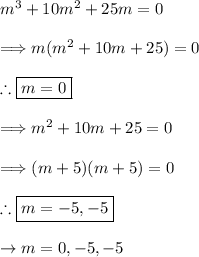
(3) - Form the appropriate general solution

`\boxed{\left\begin{array}{ccc}\text{\underline{Solutions to Higher-order DE's:}}\\\\\text{Real,distinct roots} \rightarrow y=c_1e^(m_1t)+c_2e^(m_2t)+...+c_ne^(m_nt)\\\\ \text{Duplicate roots} \rightarrow y=c_1e^(mt)+c_2te^(mt)+...+c_nt^ne^(mt)\\\\ \text{Complex roots} \rightarrow y=c_1e^(\alpha t)\cos(\beta t)+c_2e^(\alpha t)\sin(\beta t)+... \ ;m=\alpha \pm \beta i\end{array}\right}`

Notice we have one real, distinct root and one duplicate/repeated root. We can form the general solution as follows

`y(t)=c_1e^((0)t)+c_2e^(-5t)+c_3te^(-5t)\\\\\therefore \boxed{y(t)=c_1+c_2e^(-5t)+c_3te^(-5t)}`

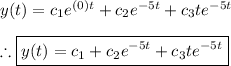
(3) - Use the initial conditions to find the values of the arbitrary constants "c_1," "c_2," and "c_3"

`y(t)=c_1+c_2e^(-5t)+c_3te^(-5t)\\\\\Rightarrow y'(t)=-5c_2e^(-5t)-5c_3te^(-5t)+c_3e^(-5t)\\\Longrightarrow y'(t)=(c_3-5c_2)e^(-5t)-5c_3te^(-5t)\\\\\Rightarrow y''(t)=-5(c_3-5c_2)e^(-5t)+25c_3te^(-5t)-5c_3e^(-5t)\\\Longrightarrow y''(t)=(25c_2-10c_3)e^(-5t)+25c_3te^(-5t)`

`\left\{\begin{array}{ccc}0=c_1+c_2\\1=c_3-5c_2\\-2=25c_2-10c_3\end{array}\right`

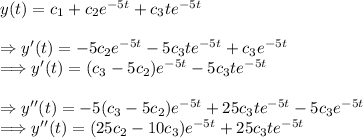
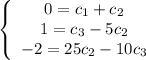
(4) - Putting the system of equations in a matrix and using a calculator to row reduce

`\left\{\begin{array}{ccc}0=c_1+c_2\\1=c_3-5c_2\\-2=25c_2-10c_3\end{array}\right \Longrightarrow\left[\begin{array}{ccc}1&1&0\\0&-5&1\\0&25&-10&\end{array}\right]=\left[\begin{array}{c}0\\1\\-2\end{array}\right] \\\\ \\\Longrightarrow \left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1&\end{array}\right]=\left[\begin{array}{c}(8)/(25) \\-(8)/(25) \\-(3)/(5) \end{array}\right]\\\\\therefore \boxed{c_1=(8)/(25) , \ c_2=-(8)/(25) , \ \text{and} \ c_3=-(3)/(5) }`

(5) - Plug in the values for "c_1," "c_2," and "c_3" to form the final solution

`\boxed{\boxed{y(t)=(8)/(25) -(8)/(25)e^(-5t)-(3)/(5)te^(-5t)}}}`