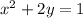Question

100 Points! Geometry question. Photo attached. Please show as much work as possible. Thank you!

Answer 1

`x^2+2y=1`

Explanation:

The equation of a parabola with a vertical axis of symmetry,

focus (h, k+p), and directrix x=h-p is given by:

`(x - h)^2 = 4p(y - k)`

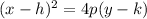
In this case, the focus is (0, 1) and the directrix is x =3.

Comparing this to the general equation,

we have

h = 0, k = 1, and x = h - p = 3.

From x = h - p, we can solve for p:

3 = 0 - p

p = -3

Substituting the values of h, k, and p into the equation, we get:

`(x - 0)^2 = 4(-3)(y - 1)`

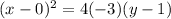
Simplifying further:

`x^2 = -12(y - 1)`

`x^2=-12y+1`

`x^2+12y=1`

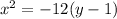
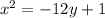
Therefore, the parabola equation is
`x^2+2y=1`