To solve the expression
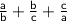 given the conditions
given the conditions
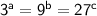 , we can use logarithmic properties and the fact that
, we can use logarithmic properties and the fact that
 and
and
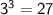 .
.
Let's start by finding the values of a, b, and c using logarithmic properties:
Taking the logarithm of both sides of
 , we get:
, we get:

Applying the power rule of logarithms, we can bring down the exponents:

Since
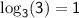 and
and
 , we simplify to:
, we simplify to:
 ---- (1)
---- (1)
Similarly, taking the logarithm of both sides of
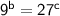 , we get:
, we get:
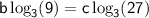
Using the values of
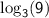 and
and
 as before, we have:
as before, we have:

Simplifying, we get:
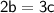 ---- (2)
---- (2)
Now, let's substitute the value of b from equation (1) into equation (2):
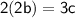

Rearranging, we find:
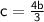 ---- (3)
---- (3)
We now have expressions for a, b, and c in terms of b. Let's substitute these into the expression
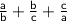 :
:

Simplifying further, we get:

Finding the common denominator and combining the fractions, we have:

Adding the fractions together, we obtain:
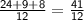
Therefore,
 .
.