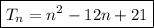Question

Given the number pattern:

20; 18: 14; 8;

a) Determine the nth term of this number pattern.
b) Determine the value of T12 in this number pattern.
c) Which term in this number pattern will have a value of - 36?

A quadratic number pattern has a second term equal to 1, a third term equal to -6 and a fifth term equal to - 14.

a) Calculate the second difference of this quadratic number pattern.
b) Hence, or otherwise, calculate the first term of this number pattern.

Answer 1

`\textsf{a)} \quad T_n=-n^2+n+20`

`\textsf{b)} \quad T_(12)=-112`

`\textsf{c)} \quad \sf 8th\;term`

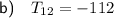
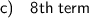
a) Second difference is 2.

b) First term is 10.

Explanation:

The given number pattern is:

• 20, 18, 14, 8, ...

To determine the type of sequence, begin by calculating the first differences between consecutive terms:

`20 \underset{-2}{\longrightarrow} 18 \underset{-4}{\longrightarrow} 14 \underset{-6}{\longrightarrow}8`

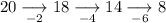
As the first differences are not the same, we need to calculate the second differences (the differences between the first differences):

`-2 \underset{-2}{\longrightarrow} -4 \underset{-2}{\longrightarrow} -6`

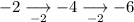
As the second differences are the same, the sequence is quadratic and will contain an n² term.

The coefficient of the n² term is half of the second difference.

As the second difference is -2, the coefficient of the n² term is -1.

Now we need to compare -n² with the given sequence (where n is the position of the term in the sequence).

`\begin{array}c\cline{1-5}n&1&2&3&4\\\cline{1-5}-n^2&-1&-4&-9&-16\\\cline{1-5}\sf operation&+21&+22&+23&+24\\\cline{1-5}\sf sequence&20&18&14&8\\\cline{1-5}\end{array}`

We can see that the algebraic operation that takes -n² to the terms of the sequence is to add (n + 20).

`\begin{array}\cline{1-5}n&1&2&3&4\\\cline{1-5}-n^2&-1&-4&-9&-16\\\cline{1-5}+n&0&-2&-6&-12\\\cline{1-5}+20&20&18&14&8\\\cline{1-5}\sf sequence&20&18&14&8\\\cline{1-5}\end{array}`

Therefore, the expression to find the the nth term of the given quadratic sequence is:

`\boxed{T_n=-n^2+n+20}`

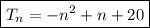
To find the value of T₁₂, substitute n = 12 into the nth term equation:

`\begin{aligned}T_(12)&=-(12)^2+(12)+20\\&=-144+12+20\\&=-132+20\\&=-112\end{aligned}`

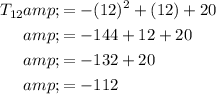
Therefore, the 12th term of the number pattern is -112.

To find the position of the term that has a value of -36, substitute Tₙ = -36 into the nth term equation and solve for n:

`\begin{aligned}T_n&=-36\\-n^2+n+20&=-36\\-n^2+n+56&=0\\n^2-n-56&=0\\n^2-8n+7n-56&=0\\n(n-8)+7(n-8)&=0\\(n+7)(n-8)&=0\\\\\implies n&=-7\\\implies n&=8\end{aligned}`

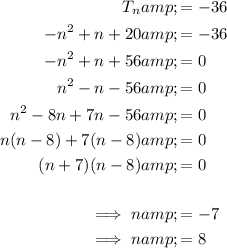
As the position of the term cannot be negative, the term that has a value of -36 is the 8th term.

`\hrulefill`

Given terms of a quadratic number pattern:

• T₂ = 1
• T₃ = -6
• T₅ = -14

We know the first differences are negative, since the difference between the second and third terms is -7. Label the unknown differences as -a, -b and -c:

`T_1 \underset{-a}{\longrightarrow} 1 \underset{-7}{\longrightarrow} -6 \underset{-b}{\longrightarrow}T_4 \underset{-c}{\longrightarrow} -14`

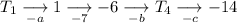
From this we can create three equations:

`T_1-a=1`

`-6-b=T_4`

`T_4-c=-14`

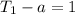
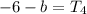
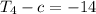
The second differences are the same in a quadratic sequence. Let the second difference be x. (As we don't know the sign of the second difference, keep it as positive for now).

`-a \underset{+x}{\longrightarrow} -7\underset{+x}{\longrightarrow} -b \underset{+x}{\longrightarrow}-c`

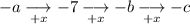
From this we can create three equations:

`-a+x=-7`

`-7+x=-b`

`-b+x=-c`

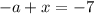
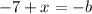
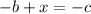
Substitute the equation for -b into the equation for -c to create an equation for -c in terms of x:

`-c=(-7+x)+x`

`-c=2x-7`

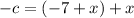
Substitute the equations for -b and -c (in terms of x) into the second two equations created from the first differences to create two equations for T₄ in terms of x:

`\begin{aligned}-6-b&=T_4\\-6-7+x&=T_4\\T_4&=x-13\end{aligned}`

`\begin{aligned}T_4-c&=-14\\T_4+2x-7&=-14\\T_4&=-2x-7\\\end{aligned}`

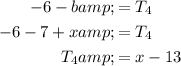
Solve for x by equating the two equations for T₄:

`\begin{aligned}T_4&=T_4\\x-13&=-2x-7\\3x&=6\\x&=2\end{aligned}`

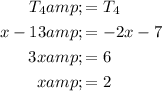
Therefore, the second difference is 2.

Substitute the found value of x into the equations for -a, -b and -c to find the first differences:

`-a+2=-7 \implies -a=-9`

`-7+2=-b \implies -b=-5`

`-5+2=-c \implies -c=-3`

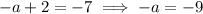
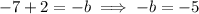
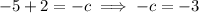
Therefore, the first differences are:

`T_1 \underset{-9}{\longrightarrow} 1 \underset{-7}{\longrightarrow} -6 \underset{-5}{\longrightarrow}T_4 \underset{-3}{\longrightarrow} -14`

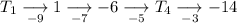
Finally, calculate the first term:

`\begin{aligned}T_1-9&=1\\T_1&=1+9\\T_1&=10\end{aligned}`

Therefore, the first term in the number pattern is 10.

`10 \underset{-9}{\longrightarrow} 1 \underset{-7}{\longrightarrow} -6 \underset{-5}{\longrightarrow}-11 \underset{-3}{\longrightarrow} -14`

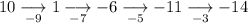
Note: The equation for the nth term is:

`\boxed{T_n=n^2-12n+21}`