Question

This number pattern -1:5 ;x; 35 ; ...

Is a quadratic number pattern.
a) Calculate x
b) Hence, or otherwise, determine the nth term of the sequence.

This sequence 4;9; x; 37; .... is a quadratic sequence.
a) Calculate x
b) Hence, or otherwise, determine the nth term of the sequence.

Answer 1

`\textsf{a)} \quad x = 17`

`\textsf{b)} \quad T_n=3n^2-3n-1`

`\textsf{a)} \quad x = 20`

`\textsf{b)} \quad T_n=3n^2-4n+5`

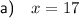
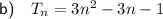
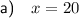
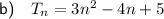
Explanation:

Given quadratic number pattern:

• -1, 5, x, 35, ...

To find the equation for the nth term, we can use the general form of a quadratic equation:

`\boxed{T_n=an^2 + bn + c}`

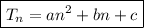
where n is the position of the term.

Let's substitute the values of T₁, T₂ and T₄ into the quadratic equation: to create three equations:

`\begin{aligned}T_1=a(1)^2+b(1)+c&=-1\\a+b+c&=-1\end{aligned}`

`\begin{aligned}T_2=a(2)^2+b(2)+c&=5\\4a+2b+c&=5\end{aligned}`

`\begin{aligned}T_4=a(4)^2+b(4)+c&=35\\16a+4b+c&=35\end{aligned}`

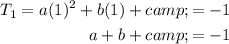
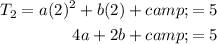
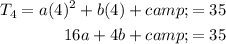
Rearrange the first equation to isolate c:

`c=-a-b-1`

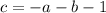
Substitute this into the second and third equations:

`\begin{aligned}4a+2b+(-a-b-1)&=5\\3a+b&=6\end{ailgned}`

`\begin{aligned}16a+4b+(-a-b-1)&=35\\15a+3b&=36\end{ailgned}`

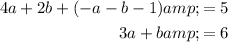
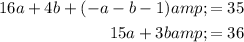
Solve the equations simultaneously by rearranged the first equation to isolate b and substituting this into the second equation and solving for a:

`b=-3a+6`

`\begin{aligned}15a+3(-3a+6)&=36 \\15a-9a+18&=36\\6a&=18\\a&=3 \end{aligned}`

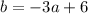
Substitute the found value of a into the equation for b and solve for b:

`\begin{aligned}b&=-3a+6\\&=-3(3)+6\\&=-9+6\\&=-3\end{aligned}`

Finally, substitute the found values of a and b into the equation for c and solve for c:

`\begin{aligned}c&=-a-b-1\\&=-3-(-3)-1\\&=-3+3-1\\&=-1\end{aligned}`

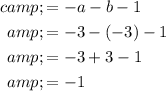
Therefore, the equation for the nth term is:

`\boxed{T_n=3n^2-3n-1}`

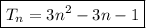
The value of x is the 3rd term. Therefore, to find the value of x, substitute n = 3 into the equation for the nth term:

`\begin{aligned}T_3&=3(3)^2-3(3)-1\\&=3(9)-3(3)-1\\&=27-9-1\\&=18-1\\&=17\end{aligned}`

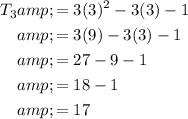
Therefore, the value of x is 17.

`\hrulefill`

Given quadratic number pattern:

• 4, 9, x, 37, ...

To find the equation for the nth term, we can use the general form of a quadratic equation:

`\boxed{T_n=an^2 + bn + c}`

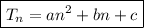
where n is the position of the term.

Let's substitute the values of T₁, T₂ and T₄ into the quadratic equation: to create three equations:

`\begin{aligned}T_1=a(1)^2+b(1)+c&=4\\a+b+c&=4\end{aligned}`

`\begin{aligned}T_2=a(2)^2+b(2)+c&=9\\4a+2b+c&=9\end{aligned}`

`\begin{aligned}T_4=a(4)^2+b(4)+c&=37\\16a+4b+c&=37\end{aligned}`

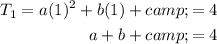
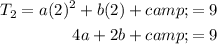
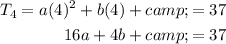
Rearrange the first equation to isolate c:

`c=-a-b+4`

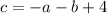
Substitute this into the second and third equations:

`\begin{aligned}4a+2b+(-a-b+4)&=9\\3a+b&=5\end{ailgned}`

`\begin{aligned}16a+4b+(-a-b+4)&=37\\15a+3b&=33\end{ailgned}`

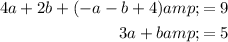
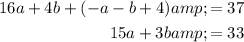
Solve the equations simultaneously by rearranged the first equation to isolate b and substituting this into the second equation and solving for a:

`b=-3a+5`

`\begin{aligned}15a+3(-3a+5)&=33 \\15a-9a+15&=33\\6a&=18\\a&=3 \end{aligned}`

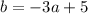
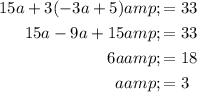
Substitute the found value of a into the equation for b and solve for b:

`\begin{aligned}b&=-3a+5\\&=-3(3)+5\\&=-9+5\\&=-4\end{aligned}`

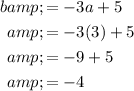
Finally, substitute the found values of a and b into the equation for c and solve for c:

`\begin{aligned}c&=-a-b+4\\&=-3-(-4)+4\\&=-3+4+4\\&=5\end{aligned}`

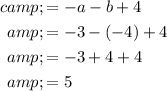
Therefore, the equation for the nth term is:

`\boxed{T_n=3n^2-4n+5}`

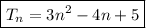
The value of x is the 3rd term. Therefore, to find the value of x, substitute n = 3 into the equation for the nth term:

`\begin{aligned}T_3&=3(3)^2-4(3)+5\\&=3(9)-4(3)+5\\&=27-12+5\\&=15+5\\&=20\end{aligned}`

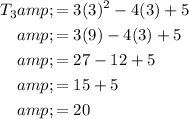
Therefore, the value of x is 20.