Question

I have 12 teams that will play each other once, but have activities that each team will only play once. How many weeks and activities do I need.

Answer 1

you will have a total of 66 games (12 + 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1).

If you have 66 games and each game is an activity that each team will play once, then you will need 66 activities.

If you want each team to have only one activity per week, then you will need 66 weeks to complete all the activities.

Answer 2

Answer: 66

==============================================

Step-by-step explanation:

The formula to use is n*(n-1)/2

Plug in n = 12 to get 12*(12-1)/2 = 12*11/2 = 132/2 = 66

That formula is from the nCr combination formula when r = 2.

---------------------

Here's a visual way to see why that rule works.

Imagine there are only 4 teams. We'll make a table that has 4 rows and 4 columns. The team names are A,B,C,D.

`\begin{array}c \cline{1-5} & A & B & C & D\\\cline{1-5}A & & & & \\\cline{1-5}B & & & & \\\cline{1-5}C & & & & \\\cline{1-5}D & & & & \\\cline{1-5}\end{array}`

In the table, cross out the cells where one team pairs up with itself. That's along the main diagonal pointing to the northwest (or southeast).

`\begin{array}c \cline{1-5} & A & B & C & D\\\cline{1-5}A & X & & & \\\cline{1-5}B & & X & & \\\cline{1-5}C & & & X & \\\cline{1-5}D & & & & X\\\cline{1-5}\end{array}`

Let's also cross out any cell below the main diagonal.

`\begin{array}c \cline{1-5} & A & B & C & D\\\cline{1-5}A & X & & & \\\cline{1-5}B & X & X & & \\\cline{1-5}C & X & X & X & \\\cline{1-5}D & X & X & X & X\\\cline{1-5}\end{array}`

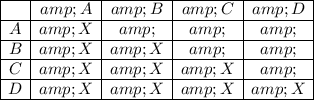
We do this because a mirrored copy is found above the diagonal.

We started with 4*4 = 16 cells. Then subtracted off the diagonal to get 16-4 = 12 cells left over. Then divide in half because we crossed off the lower half to get 12/2 = 6 different matchups among the 4 teams.

Those 6 matchups are:

1. A vs B
2. A vs C
3. A vs D
4. B vs C
5. B vs D
6. C vs D

The order doesn't matter. A matchup like "A vs B" is the same as "B vs A".

We'll take this concept to extend it to n teams. We have n*n = n^2 cells to start with. Subtract off the n cells along the diagonal to get n^2-n = n(n-1) cells remaining.

Then we split that in half to get the formula n(n-1)/2.