Question

The lengths of the bases of a right trapezoid are 9 cm and 18 cm. The length

of a longer leg is 15 cm. Find the area of the trapezoid.

Answer 1

Firstly, we will draw figure

now, we will draw a altitude from B to DC that divides trapezium into rectangle and right triangle

because of opposite sides of rectangle ABMD are congruent

so,

DM = AB = 9

CM = CD - DM

CM = 18 - 9

CM = 9

now, we can find BM by using Pythagoras theorem

`\sf BM=√(BC^2-CM^2)`

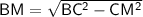
now, we can plug values

we get

`\sf BM=√(15^2-9^2)`

`\sf BM=12`

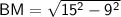
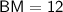
now, we can find area of trapezium

`A=\sf (1)/(2)(AB+CD)*(BM)`

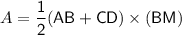
now, we can plug values

and we get

`A=\sf (1)/(2)(9+18)*(12)`

`A=\sf 162 \ cm^2`

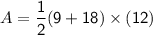
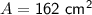
So, area of of the trapezoid is 162 cm^2

Answer 2

To find the area of a trapezoid, you can use the formula A = (a + b) * h / 2, where A is the area, a and b are the lengths of the bases, and h is the height.

In this case, the lengths of the bases are given as 9 cm and 18 cm, and the longer leg (the height) is given as 15 cm.

Substituting the values into the formula:

A = (9 cm + 18 cm) * 15 cm / 2
A = 27 cm * 15 cm / 2
A = 405 cm² / 2
A = 202.5 cm²

Therefore, the area of the trapezoid is 202.5 square centimeters.

I hope this helps! :)