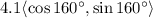Question

Given the vector u equal to 2 (cos 325°, sin 325°) and vector v equal to

6 (cos 155°, sin 155°), find the sum u + v and write your answer in
magnitude and direction form with the magnitude rounded to the nearest
tenth and the direction rounded to the nearest degree, 0° ≤ 0 < 360°.

Answer 1

`u+v=4.1\langle\cos160^\circ,\sin160^\circ\rangle`

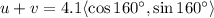
Explanation:

When adding two vectors, we add their horizontal components, and then their vertical components:

`u=2\langle\cos325^\circ,\sin325^\circ\rangle=\langle2\cos325^\circ,2\sin325^\circ\rangle\\v=6\langle\cos155^\circ,\sin155^\circ\rangle=\langle6\cos155^\circ,6\sin155^\circ\rangle\\\\u+v=\langle2\cos325^\circ+6\cos155^\circ,2\sin325^\circ+6\sin155^\circ\rangle\\u+v\approx\langle-3.8,1.39\rangle`

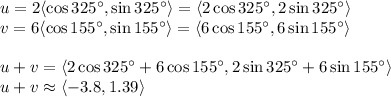
We are not done however as we need to now calculate the magnitude and the direction of the resultant vector:

Magnitude:

`||u+v||=√((-3.8)^2+1.39^2)\approx4.1`

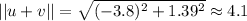
Direction:

`\displaystyle \theta=tan^(-1)\biggr((1.39)/(-3.8)\biggr)\approx-20^\circ=180-20^\circ=160^\circ`

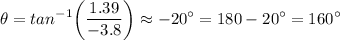
Therefore, the resultant vector is about
`4.1\langle\cos160^\circ,\sin160^\circ\rangle`