Question

Hi! I usually wouldn't ask for homework help but I have been stuck on this section for quite a few hours now and I'm really unsure as to how I should answer it. Thank you! :)

Answer 1

1) 5/6
2) 19/30
3) They are mutually exclusive.

Explanation:

Let's break the diagram down.
We have four types of smoothies:

Contains apple but not blueberry - 12
Contains blueberry but not apple - 7
Contains both blueberry and apple - 3
Doesn't contain either - 8

From here, we find that there are 30 smoothies in total.

In addition, we know that the number of smoothies containing an apple is 15, and the number of smoothies containing blueberry is 10.

Therefore,

`P(\text{contains apple}) = \frac{\text{contains apple}}{\text{total}} = (15)/(30) = \frac12\\\\P(\text{contains blueberry}) = \frac{\text{contains blueberry}}{\text{total}} = (10)/(30) = \frac13\\\\\text{a) } P(\text{contains apple}) + P(\text{contains blueberry}) = \frac12 + \frac13 = \frac36 + \frac26 = \frac56`

Now, the probability of getting apple OR strawberry is given by adding the probabilities of getting one of the flavors but not the other.

`P(\text{apple, no blueberry}) = (12)/(30)\\\\P(\text{blueberry, no apple}) = (7)/(30)\\\\P(\text{apple or blueberry}) = (12)/(30) + \frac7{30} = (19)/(30)`

We can check if the events are mutually exclusive using the formula:

`P(A \cup B) = P(A) + P(B) - P(A \cap B)`
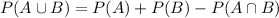
In our case, A means contains apple, and B means contains blueberry.

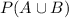`P(A \cup B)` resembles the case for exclusively apple or exclusively blueberry (AKA our answer for b).

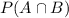`P(A \cap B)` resembles the case for both apple and blueberry (AKA the intersection), which is equal to 3/30 = 1/10.

If the two sides are equal, the cases are not mutually exclusive.

`(19)/(30) = (15)/(30) + (10)/(30) - (3)/(30)\\\\(19)/(30) \\e (22)/(30)`

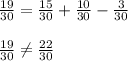
Therefore, the events are mutually exclusive.