Question

A helium-filled weather balloon has a volume of 879 L at 21.9°C and 759 mmHg. It is released and rises to an altitude of 8.70 km, where the pressure is 281 mmHg and the temperature is –35.1°C. The volume of the balloon at this altitude is

Answer 1

The volume of the balloon at an altitude of 8.70 km is approximately 1915.33 liters.

To determine the volume of the balloon at an altitude of 8.70 km, we will use the combined ideal gas law, which relates the pressure, volume, and temperature of a gas.

The combined ideal gas law is a mathematical relationship that relates the pressure, volume, and temperature of a gas. This law is a combination of Boyle's, Charles', and Gay-Lussac's laws, and is used to describe the behavior of gases under ideal conditions.

The combined ideal gas law is:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{ (P_1* V_1)/(T_1)=(P_2* V_2)/(T_2) } \end{gathered}$} }`

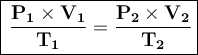
Where:

• P₁ = initial pressure
• V₁ = initial volume
• T₁ = initial temperature
• P₂ = ultimate pressure
• V₂ = final volume
• T₂ = final temperature

First, we'll convert the temperatures to Kelvin by adding 273 to the Celsius values:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_1=21.9 \ ^(\circ)C+273 = 294.9 \ K} \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{T_2=-35.1 \ ^(\circ)C+273 = 237.9 \ K} \end{gathered}$} }`

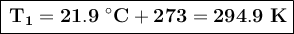
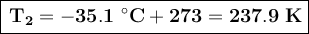
We clear our formula for formula to calculate the final volume.

The clear formula is:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=(P_1* V_1* T_2)/(P_2* T_1) } \end{gathered}$}}`

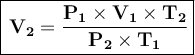
Where:

• P₁ = initial pressure
• V₁ = initial volume
• T₁ = initial temperature
• P₂ = ultimate pressure
• V₂ = final volume
• T₂ = final temperature

Substituting the known values into the formula, we get:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=\frac{(759\\ot{mmHg}*879 \ L*237.9\\ot{k}) }{281\\ot{mmHg}*294.9\\ot{k} } } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2=(158717601.9 \ L)/(82866.9 ) } \end{gathered}$} }`

`\boxed{\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_2\approx1915.33 \ L } \end{gathered}$} }}`

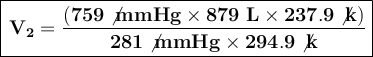
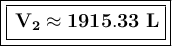
The volume of the balloon at an altitude of 8.70 km is approximately 1915.33 liters.