Convert the rectangular coordinates (–6, 6) to polar coordinates.

Question

asked May 24, 2024 76.7k views

2 Answers

Holyredbeard · Answer 1 · 2024-05-27T07:09:27+0000

The polar coordinates are (6(
$\sqrt[]{2}$ , 3pi/4).

Rectangular coordinates are in the form of (x, y) and Polar coordinates are expressed in the form of (r,
$\theta$ ).

x = r cos(
$\theta$ ), y = r sin(
$\theta$ ) and x^2 +y^2 =r^2 ...(1)

So by using above formulas we can solve our question.

Here , x= -6 and y= 6

r^2 = (-6)^2 +(6)^2

=72

=>r = 6(
$\sqrt[]{2}$ )

Put the values of x and y in the mentioned formula in eq(1)

-6 = 6(
$\sqrt[]{2}$ )cos
$\theta$

6 = 6(
$\sqrt[]{2}$ )sin(
$\theta$ ),

=>-1/(
$\sqrt[]{2}$ = cos(
$\theta$ ) , 1/
$\sqrt[]{2}$ = sin
$\theta$

Here cos is negative and sin is positive so it lies in 2nd quadrant

so here
$\theta$ lies between
$(\pi)/(2) \leq\theta\leq\pi$

$\theta$ = π-π/4

=3π/4

So,(r,
$\theta$ ) = ( 6√2,
$(3\pi)/(4)$ )

Shaqwan · Answer 2 · 2024-05-29T21:24:09+0000

Answer: A Polar is (6√2,
$(3\pi )/(4)$ )

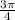Explanation:

Draw a line to point (see image). You need to find the length of that line and then the angle. Polar(length, angle)

Using pythagorean theorem

length² = (6)² + (-6)²

length² = 36 +36

length =√72

length =
√(36 *2)

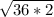
length = 6√2

To find angle:

The triangle size is 6-6-6√2 Let's proportionally shrink so we can use unit circle numbers to figure angle. Becomes: 1-1-√2

So when we do sin x = opp/adj

sin x =
(1)/(√(2) ) >get rid of radical on bottom

sin x =
(√(2) )/(2) > when is sin =
This happens at
$(\pi )/(4)$ but we are in the 2nd quadrant so the angle is
$(3\pi )/(4)$

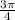
Polar is (6√2,
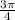$(3\pi )/(4)$ )