Question

What are the two solutions to the following equation? d squared/4 +43=52

Answer 1

d = ± 6

Step-by-step explanation

Our equation is:

`\sf{(d^2)/(4)+43=52}`

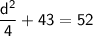
Subtract 43 from each side

`\sf{(d^2)/(4)=9}`

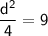
Next, we have to get rid of the fraction on the left side, which we do by multiplying each side by 4:

`\sf{d^2=36}`

The last step is to square-root each side. Keep in mind that this will give us two solutions that are opposites of each other.

`\sf{d=6, d = -6}`

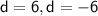
This phenomenon is explained below.

When we square 6, we get 36. But when we square -6, we also get 36. This gives us 36 when we take its square root.

Hence, d = ± 6 (d = 6, d = -6)

Answer 2

d = 6, -6

Explanation:

`(d^(2) )/(4)` + 43 = 52

`(d^(2) )/(4)` = 9

Multiply both sides of the equation by 4.

d² = 36

d = ± √36

d = ± 6

So, d = 6, -6