Question

The line PQ has equation 3x - 2y = 12 Pis the point with coordinates (6, 3) and Q is the point with coordinates (- 2, k)

a) Find the value of k.

Answer 1

k = - 9

Explanation:

the equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

given equation of PQ is

3x - 2y = 12 ( subtract 3x from both sides )

- 2y = - 3x + 12 ( divide through by - 2 )

y =
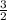`(3)/(2)` x - 6 ← in slope- intercept form

with slope m =
`(3)/(2)`

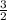
now calculate the slope of PQ using the slope formula and equate to
`(3)/(2)`

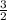
m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

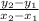
with (x₁, y₁ ) = P (6, 3 ) and (x₂, y₂ ) = Q (- 2, k )

m =
`(k-3)/(-2-6)` =
`(k-3)/(-8)`

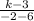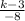
equating the slopes of PQ

`(k-3)/(-8)` =
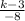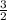`(3)/(2)` ( cross- multiply )

2(k - 3) = - 8 × 3 = - 24 ( divide both sides by 2 )

k - 3 = - 12 ( add 3 to both sides )

k = - 9