Answer:

Explanation:
Let x be the denominator.
If the numerator is 2 less than the denominator, then the expression for the numerator is (x - 2):

If 3 is added to both the numerator and the denominator, and the answer is 5/6, then:
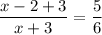
Now we can solve the equation for x.
Simplify the numerator in the fraction on the left of the equation:
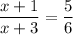
Cross mutliply:
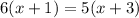
Expand the brackets:

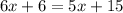
Subtract 5x from both sides of the equation:
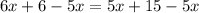

Subtract 6 from both sides of the equation:
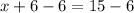
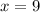
Therefore, the value of x is 9.
Now substitute the found value of x into the original rational expression:

Therefore, the original fraction is:
