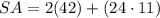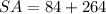Answer:
348 cm²
Explanation:
In this problem, we are asked to find the surface area of the regular hexagonal prism. We can use the formula:

where
 is the area of the prism's hexagonal faces,
is the area of the prism's hexagonal faces,
 is the perimeter of the hexagonal faces, and
is the perimeter of the hexagonal faces, and
 is the prism's height.
is the prism's height.
We can solve for the area of the hexagonal faces by splitting it into 6 triangles and multiplying the area of each triangle by 6.
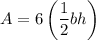
where
 is the triangle's base and
is the triangle's base and
 is the triangle's height.
is the triangle's height.
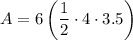
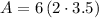

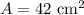
We can solve for the perimeter by multiplying one side length by 6.

We are given that the height of the prism is 11 cm.

Finally, we can solve for the surface area of the prism by plugging these values into the above formula.