Question

The position (in meters) of a particle per respect to time (in seconds) is defined by the following function: s(t) = t^4 - 16t^3 + 72t^2 +5. Find the maximal and minimal value for the speed of the particle on domain of t being [1,7[

Answer 1

Max at t=2, 128 m/s

Min at t=6, 0 m/s

Explanation:

Given the position function of a particle with respect to time, find the minimum and maximum velocity the particle travels over the interval [1,7].

`s(t)=t^4-16t^3+72t^2+5`

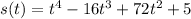
(1) - Find the velocity function of the particle

The velocity function is a derivative of the position function.

`s'(t)=v(t)\\\\s(t)=t^4-16t^3+72t^2+5\\\\\Longrightarrow s'(t)=(d)/(dx)[t^4-16t^3+72t^2+5] \\\\\text{Use the derivative rules.}\\\\\boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\(d)/(dx)[x^n]=nx^(n-1) \end{array}\right} \ \ \boxed{\left\begin{array}{ccc}\text{\underline{Constant Rule:}}\\\\(d)/(dx)[k]=0 \end{array}\right} \\\\\\\Longrightarrow s'(t)=(4)t^(4-1)-16(3)t^(3-1)+72(2)t^(2-1)+0\\\\\Longrightarrow s'(t)=4t^(3)-48t^(2)+144t\\\\`

`\therefore \boxed{v(t)=4t^(3)-48t^(2)+144t}`

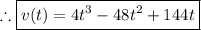
(3) - Take the derivative of v(t)

`v(t)=4t^(3)-48t^(2)+144t\\\\\Longrightarrow v'(t)=12t^2-96t+144`

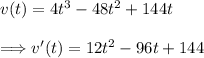
(4) - Let v'(t)=0 and solve for "t," these are the critical points

`v'(t)=12t^2-96t+144\\\\\Longrightarrow 0=12t^2-96t+144\\\\\Longrightarrow 0=12[t^2-8t+12]\\\\\Longrightarrow 0=t^2-8t+12\\\\\Longrightarrow (t-6)(t-2)=0\\\\\therefore \text{The critical points are} \ \boxed{t=6 \ \text{and} \ t=2}`

(5) - Find the max/min values (in this case these values represent the particle's velocity) by plugging the critical points into v(t)

`\text{Recall that} \ v(t)=4t^(3)-48t^(2)+144t \ \text{and} \ t=6, \ t=2\\\\\text{\underline{When t=6:}}\\\\\Longrightarrow v(6)=4(6)^(3)-48(6)^(2)+144(6)\\\\\Longrightarrow \boxed{v(6)=0 \ m/s}\\\\\text{\underline{When t=2:}}\\\\\Longrightarrow v(2)=4(2)^(3)-48(2)^(2)+144(2)\\\\\Longrightarrow \boxed{v(6)=128 \ m/s}`

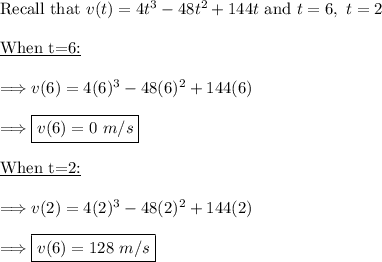
Thus, at time, t=6, the particle's velocity is smallest, 0 m/s. And at time, t=2, the particle's velocity is greatest, 128 m/s.