Question

The square root of the sum of twice a number and 3 is 6. find the number​

Answer 1

`(33)/(2)`

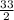
Explanation:

In the problem, "The square root of the sum of twice a number and 3 is 6" can be converted to an equation that looks like this:

Let x be the number:

`√(2x+3 = 6 )`

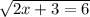
In order to solve the problem:

`√(2x+3)^2=6^2`

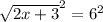
By squaring both sides to remove the exponent:

`{2x + 3 = 36}`

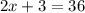
Simplify:

`{2x+3-3=36-3}`

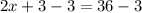
Subtract 3 from both sides:

`{2x = 33 }`

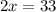
Then Simplifying further:

`(2x)/(2) = (33)/(2)`

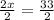
Divide both sides by 2 to remove 2 from the x.

`{x = (33)/(2) }`

Thus, meaning the answer is
`(33)/(2)`

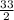
Hope this helps you.

Answer 2

Answer in fraction form = 33/2

Answer in decimal form = 16.5

===========================================================

Work Shown:

n = some number

2n = twice that number

2n+3 = "sum of twice a number and 3"

`√(2n+3)` = square root of the previous expression

The equation we need to solve is
`√(2n+3) = 6`

We'll follow PEMDAS in reverse, undoing each operation, to isolate n

`√(2n+3) = 6\\\\\left(√(2n+3)\right)^2 = 6^2 \ \ \text{ ... square both sides}\\\\2n+3 = 36\\\\2n+3-3 = 36-3 \ \ \text{ ... subtract 3 from both sides}\\\\2n = 33\\\\(2n)/(2)=(33)/(2) \ \ \text{ ... divide both sides by 2}\\\\n = (33)/(2)\\\\n = 16.5`