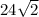Question

a square garden has a diagonal of 12 m. What is the perimeter of the garden? Express in simplest radical form

Answer 1

The perimeter of the garden, in meters, is
`24√(2)`

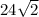
Explanation:

Diagonal of a square:

The diagonal of a square is found applying the Pythagorean Theorem.

The diagonal of the square is the hypothenuse, while we have two sides.

Diagonal of 12m:

This means that
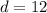`d = 12`, side s. So

`s^2 + s^2 = 12^2`

`2s^2 = 144`

`s^2 = (144)/(2)`

`s^2 = 72`

`s = √(72)`

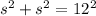
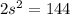
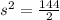
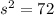
Factoring 72:

Factoring 72 into prime factors, we have that:

72|2

36|2

18|2

9|3

3|3

1

So

`72 = 2^(3)*3^(2)`

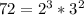
So, in simplest radical form:

`s = √(72) = \sqrt{2^(3)*3^(2)} = √(2^3)*√(3^2) = 2√(2)*3 = 6√(2)`

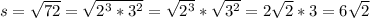
Perimeter of the garden:

The perimeter of a square with side of s units is given by:

`P = 4s`

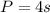
In this question, since
`s = 6√(2)`

`P = 4s = 4*6√(2) = 24√(2)`

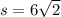
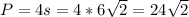
The perimeter of the garden, in meters, is
`24√(2)`