Answer:
about 11.598 meters
Explanation:
For this situation, we will primarily rely on the Pythagorean theorem.
We can draw a (straight) 10-meter line between Tim and the tree in order to further understand the problem. Since Tim and the tree are both standing straight, a perceived line will be parallel to the ground. Another line can be drawn between Tim's eyes and the top of the tree. Please view the attached image for reference. Using the Pythagorean theorem (
 ), we can substitute 10 for a and 14 for c ---> giving us
), we can substitute 10 for a and 14 for c ---> giving us
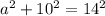 or
or
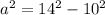 . We then subtract--->
. We then subtract--->
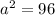 and square root both sides to get a, which is equal to about 9.798 meters. However, this is only the height from Tim's eye level; therefore, to it, we must add 1.8 meters.
and square root both sides to get a, which is equal to about 9.798 meters. However, this is only the height from Tim's eye level; therefore, to it, we must add 1.8 meters.
Our final solution is: about 11.598 meters.