Answer:
The width of the flower bed is 3.5 m
Explanation:
- Let x represent the width of the flower bed in meters.
- The length of the lawn along with the flower bed would be increased by 2x (flower bed on both sides), and the width of the lawn along with the flower bed would be increased by 2x as well.
- So, the length of the rectangular region including the flower bed would be (2x + 8) m as x + x + 8 = 2x + 8.
- The width would be (2x + 4) meters as x + x + 4 = 2x + 4.
- We know that the area of the rectangular region including the flower bed is the combined area of the lawn and flower bed, which is given as 165 square meters. Therefore, we can use the following equation to find x, the width of the flower bed:
(2x + 8) * (2x + 4) = 165
Step 1: Expand equation by multiplying and adding 2x * 2x, 2x * 4, 8 * 2x, and 8 * 4:
(2x * 2x) + (2x * 4) + (8 * 2x) + (8 * 4) = 165
2x^2 + 8x + 16x + 32 = 165
2x^2 + 24x + 32 = 165
Step 2: Subtract 165 from both sides to prepare quadratic for solving:
(2x^2 + 24x + 32 = 165) - 165
2x^2 + 24x - 133 = 0
Step 3: Solve with quadratic equation:
Currently 2x^2 + 24x - 133 = 0 in standard form, whose general equation is:
ax^2 + bx + c = 0
Thus, in 2x^2 + 24x - 133 = 0, 2 is a, 24 is b, and -133 c.
The quadratic equation is:
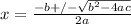
(Remember that the +/- comes from the fact that there can be both a positive and negative solution to a quadratic.
Let's find the positive solution then the negative solution:
Step 4: Find positive solution:

Step 5: Find negative solution:
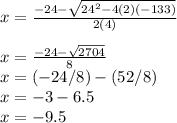
We can't have a negative measure, so the width of the flower bed is 3.5 m.
Optional Step 6: Check validity of answer:
We can check that 3.5 is the correct answer by plugging in 3.5 for x in (2x + 8)(2x + 4) = 165 and checking that we get 165 on both sides:
(2 * 3.5 + 8)(2 * 3.5 + 4) = 165
(7 + 8)(7 + 4) = 165
(15)(11) = 165
165 = 165
Thus, our answer is correct.