Answer:
Approximately
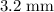 .
.
Step-by-step explanation:
In diffraction, dark fringes (minimum) are observed when light from the two slits interfere destructively. These interferences require a phase difference of
 cycle. At the
cycle. At the
 th minimum, the path difference would needs to be
th minimum, the path difference would needs to be
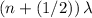 (for integer values of
(for integer values of
 .)
.)
Let
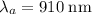 and
and
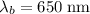 denote the wavelength of the two waves. Assume that the
denote the wavelength of the two waves. Assume that the
 th minimum of the
th minimum of the
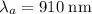 wave coincides with the
wave coincides with the
 th minimum of the
th minimum of the
 wave. (Both
wave. (Both
 and
and
 are non-negative integers.)
are non-negative integers.)
The path difference of the two waves need to match:
 .
.
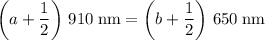 .
.
In other words, the value of non-negative integers
 and
and
 need to satisfy:
need to satisfy:
 .
.
There might be more than one pairs of
 and
and
 that satisfy the constraints. In general, the least positive
that satisfy the constraints. In general, the least positive
 that meets the requirements can be found using linear programming techniques.
that meets the requirements can be found using linear programming techniques.
Specifically in this example, note that:
 .
.
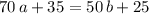 .
.
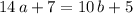 .
.
The least positive value of
 that satisfy the requirements is
that satisfy the requirements is
 , for which
, for which
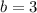 .
.
At the position where minimum of the two waves coincide, path difference would be:
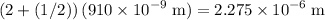 for the
for the
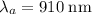 wave, which is the same as
wave, which is the same as
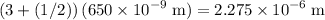 for the
for the
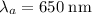 wave.
wave.
In double-slit diffraction, for a pattern generated from a path difference of
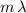 , the angle
, the angle
 between that pattern and the central maximum (relative to the center of the slits) should satisfy:
between that pattern and the central maximum (relative to the center of the slits) should satisfy:
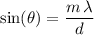 ,
,
Where
 is the distance between (the center of) the two slits.
is the distance between (the center of) the two slits.
Rearrange to obtain:
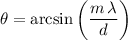 .
.
In this question, the path difference is
 , while the distance between the two slits is
, while the distance between the two slits is
 . The angle between the pattern on the screen and the central maximum should be:
. The angle between the pattern on the screen and the central maximum should be:
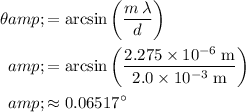 .
.
Since the screen is at a distance of
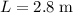 from the screen, the on-screen distance
from the screen, the on-screen distance
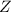 between the central maximum and the pattern at
between the central maximum and the pattern at
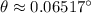 would be:
would be:
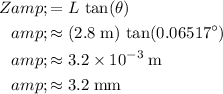 .
.