Answer: Exactly 1 solution
=============================================================
Step-by-step explanation:
When two lines have different slopes like this, it means the two lines are not parallel. Recall parallel lines are when the slopes are equal (the rise and run are the same, so you can think of it like the same stair-step pattern).
Non-parallel lines intersect at exactly one location. This point of intersection is the solution to the system of equations.
----------------------------
A more in-depth look (optional section)
Let's consider the system of equations shown below
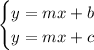
For each equation shown here, the m values are the same slope. However, b and c are different values (in other words,
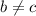 ). This system describes any two parallel lines that aren't vertical.
). This system describes any two parallel lines that aren't vertical.
Since we're dealing with the same y value, we can apply substitution to try to solve for x. But we run into a problem
y = mx+b
mx+c = mx+b ... replace y with mx+c
c = b .... subtract mx from both sides
But we stated that c and b were different, and not equal. This is a contradiction. So if we had a system of this form, then we have 2 parallel lines that lead to no solution. We call this an inconsistent system.
Next, we'll consider this system of equations
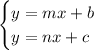
The only thing different here is the second equation has n instead of m as its slope. We'll assume that m and n are not equal to each other. If m = n, then we just end up with the previous scenario. Let's try to solve x now
y = mx+b
nx+c = mx+b
nx-mx = b-c
(n-m)x = b-c
x = (b-c)/(n-m)
Assuming
 , we can generate one solution for x as shown above. This single solution for x generates a corresponding single solution for y. So overall, this proves that we have one ordered pair (x,y) solution to this system.
, we can generate one solution for x as shown above. This single solution for x generates a corresponding single solution for y. So overall, this proves that we have one ordered pair (x,y) solution to this system.
In short, I've shown that if m and n are different slopes, then the system of equations has exactly one solution.