Question

15 POINTS

Solve the system using substitution

Answer 1

Answer: (1, -2)

Explanation:

In order to solve a system of equations, you have to solve for x and y by substituting or eliminating

3x - 4y = 11

y + 3x =1 >This equation looks easiest to rearrange to substitute.

Move the 3x to other side by subtracting 3x from both

sides

y= 1 -3x >Sub substitute this in to the first equation

3x - 4( 1 - 3x) = 11 >Distribute -4

3x -4 + 12x = 11 > Combine like terms

15x - 4 = 11 > Add 4 to both sides

15x = 15 >Divide both sides by 15

x=1 >substitute back into either equation to

solve for y

y + 3(1) =1

y + 3 = 1 >subtract 3 from both sides

y = -2

(1, -2)

Answer 2

(1, -2)

Explanation:

To solve this system of equations using substitution, we first need to define one variable in terms of the other.

`\begin{cases} 3x - 4y = 11 && \ \,y + 3x = 1\end{cases}`

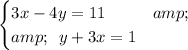
We can achieve this in the first equation by adding 4y to both sides.

`3x - 4y = 11\\\text{ } \ \ \ \, \underline{+4y} \ \ \ \ \underline{+4y}`

`3x = 11 + 4y`

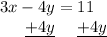
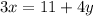
Now, we have 3x defined in terms of y, so we can substitute its definition for the 3x in the second equation.

`y + 3x = 1`

↓ substituting the definition of 3x

`y + (11 + 4y) = 1`

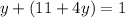
↓ combining like terms

`5y + 11 = 1`

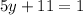
↓ subtracting 11 from both sides

`5y = -10`

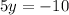
↓ dividing both sides by 5

`\boxed{y = -2}`

So, the y-coordinate of the solution to the system of equations is -2.

Next, we can solve for the x-coordinate by substituting that y-value back into one of the equations.

`y + 3x = 1`

↓ substituting -2 for y

`-2 + 3x = 1`

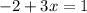
↓ adding 2 to both sides

`3x = 3`

↓ dividing both sides by 3

`\boxed{x = 1}`

So, the x-coordinate of the solution to the system of equations is 1.

We finally know both of the coordinates of the solution, so we can group them together in an ordered pair in the form (x, y):

(1, -2)