Question

A projectile is launched at 30° above ground level. what other angle at the same speed will result in the same range?

Answer 1

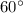`60^(\circ)` (assuming that air resistance is negligible.)

Step-by-step explanation:

Let
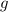`g` denote the gravitational field strength. If air resistance on the projectile is negligible:

• Vertical acceleration of the projectile will be constantly
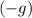  `(-g)`. In other words,
  `a_(y) = (-g)`.
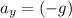• Horizontal velocity of the projectile will be constant.

Let
`\theta` denote the angle at which the projectile is launched. Let
`v` denote the initial velocity of the projectile:

• Initial vertical velocity of the projectile will be
  `u_(y) = v\, \sin(\theta)`.
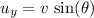• Initial horizontal velocity of the projectile will be
  `u_(x) = v\, \cos(\theta)`.

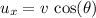Also because air resistance is negligible, vertical velocity of the projectile will be
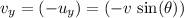`v_(y) = (-u_(y)) = (-v\, \sin(\theta))` right before the projectile lands. In other words, while the projectile was in the air, the change in vertical velocity would be
`(-v\, \sin(\theta)) - (v\, \sin(\theta)) = (-2\, v\, \sin(\theta))`.

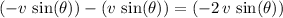Divide the change in velocity by acceleration to find the duration of the flight:

`\begin{aligned}t &= (v_(y) - u_(y))/(a_(y)) \\ &= ((-v\, \sin(\theta)) - (v\, \sin(\theta)))/((-g)) \\ &= ((-2\, v\, \sin(\theta)))/((-g)) \\ &= (2\, v\, \sin(\theta))/(g)\end{aligned}`.

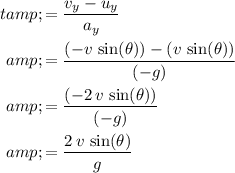Range measures the horizontal distance that this projectile has travelled. At a constant horizontal velocity of
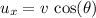`u_(x) = v\, \cos(\theta)`, this projectile would travel a distance of:

`\begin{aligned}(\text{range}) &= u_(x)\, t \\ &= (v\, \cos(\theta))\left((2\, v\, \sin(\theta))/(g)\right) \\ &= (2\, v^(2)\, \sin(\theta)\, \cos(\theta))/(g)\end{aligned}`.

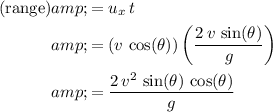Apply the double angle identity
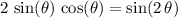`2\, \sin(\theta) \, \cos(\theta) = \sin(2\, \theta)` to further simplify this expression:

`\begin{aligned}(\text{range}) &= \cdots \\ &= (2\, v^(2)\, \sin(\theta)\, \cos(\theta))/(g) \\ &= (v^(2)\, (2\, \sin(\theta)\, \cos(\theta)))/(g) \\ &= (v^(2)\, \sin(2\, \theta))/(g)\end{aligned}`.

Note that in this question,
`v^(2)` and
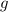`g` are both constant. Hence, for another angle of elevation
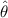`\hat{\theta}`, the range of the projectile will be the same as long as
`\sin(2\, \hat{\theta}) = \sin(2\, \theta)`.

`\sin(2\, \hat{\theta}) = \sin(2\, (30^(\circ)))`.

Since
`0^(\circ) \le \hat{\theta} \le 90^(\circ)`,
`0^(\circ) \le 2\, \hat{\theta} \le 180^(\circ)`:

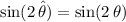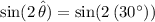`\sin(2\, \hat{\theta}) = \sin(180^(\circ) - 2\, \hat{\theta}) = \sin(2\, (90^(\circ) - \hat{\theta}))`.

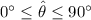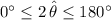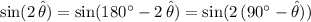Therefore,
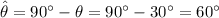`\hat{\theta} = 90^(\circ) - \theta = 90^(\circ) - 30^(\circ) = 60^(\circ)` will ensure that
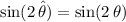`\sin(2\, \hat{\theta}) = \sin(2\, \theta)`. Launching the projectile at
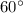`60^(\circ)` will reach the same range.

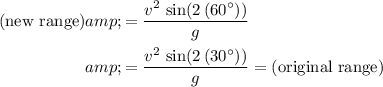`\begin{aligned}(\text{new range}) &= (v^(2)\, \sin(2\, (60^(\circ))))/(g) \\ &= (v^(2)\, \sin(2\, (30^(\circ))))/(g) = (\text{original range})\end{aligned}`.