Question

Write an equation for the linear function f satisfying the given conditions f(1) = -2 and f(4) = 7

Answer 1

f(x) = 3x -5

Explanation:

Pre-Solving

We are given a function.

We want to find the equation of this function.

• We know it is linear.
• We also know that if x = 1, f(x) = -2 and if x = 4, f(x) = 7 (that is what f(1) = -2 and f(4) = 7) mean.

We will write the equation of this function in slope-intercept form (even though there are other ways to write it). Slope-intercept form is given as f(x) = mx+b, where m is the slope and b is the value of y at the y-intercept.

Solving

We first should put our values into points.

f(1) = -2 is (1, -2) and f(4) = 7 is (4, 7).

Now, we need to find the slope of the line.

The slope (m) can be found using
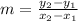`m=(y_2-y_1)/(x_2-x_1)`, where
`(x_1,y_1)` and
`(x_2,y_2)` are points.

Before we calculate m, let's label the values of the points to avoid any possible confusion.

`x_1=1\\y_1=-2\\x_2=4\\y_2=7`

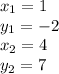
Now substitute:

`m=(y_2-y_1)/(x_2-x_1)`

`m=(7--2)/(4-1)`

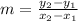
Simplify.

`m=(7+2)/(4-1)`

`m=(9)/(3)`

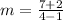
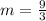
m = 3

The slope of the function is 3.

Here's our function so far:

f(x) = 3x + b

We now need to find b.

As the points (1, -2) and (4, 7) pass through the function, we can use their values to help solve for b.

We can take either one, but let's take (1, -2).

Substitute 1 as x and -2 as f(x).

-2 = 3(1) + b

Multiply.

-2 = 3 + b

Subtract.

-5 = b

Substitute -5 as b into the function.

f(x) = 3x - 5