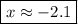Question

Solve the equation (Look at pic)

Answer 1

`x = (-3 \pm √(185))/(8)`

`x \approx 1.3 \text{ or }`
`-2.1`

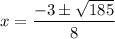
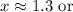
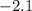
Explanation:

We can solve for x in the given equation by completing the square.

First, we can move all of the terms containing an x to one side.

`5x^2 - 6x - 11 = x^2 - 9x`

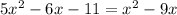
↓ subtracting x² from both sides

`4x^2 - 6x = -9x`

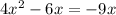
↓ adding 9x to both sides

`4x^2 + 3x + 11 = 0`

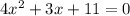
Then, we can move the non-x term to the other side.

↓ adding 11 to both sides

`4x^2 + 3x = 11`

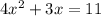
Now, we can complete the square.

↓ dividing both sides by 4 to make the x² term's coefficient 1

`x^2 + (3)/(4)x = (11)/(4)`

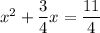
↓ adding (3/8)² to both sides

`x^2 + (3)/(4)x + (9)/(64) = (11)/(4) + (9)/(64)`

↓ factoring the perfect square

`\left(x + (3)/(8)\right)^2 = (185)/(64)`

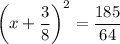
↓ taking the square root of both sides

`x + (3)/(8) = \pm\sqrt{(185)/(64)}`

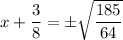
Remember that
`\text{if } x^2 = a,\text{ then } x = \pm a \text{ because } a^2 = x \text{ and } (-a)^2 = x`

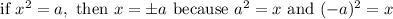
↓ subtracting 3/8 from both sides

`x = -(3)/(8) \pm(√(185))/(8)`

↓ simplifying

`\boxed{x = (-3 \pm √(185))/(8)}`

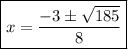
Finally, we can approximate x using a calculator.

`\boxed{x \approx 1.3}`

OR

`\boxed{x \approx -2.1}`