First we have to factorise the denominator
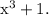
It can be factorised as,
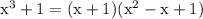
Then the fraction can be written as,
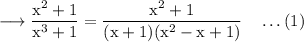
This fraction can be resolved into partial fractions by writing it as the sum of a fraction having denominator
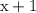 and a fraction having denominator
and a fraction having denominator
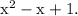
Since
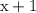 is a first degree polynomial, the numerator of the fraction having this term as denominator should be a zero degree polynomial, or a constant term, assumed as
is a first degree polynomial, the numerator of the fraction having this term as denominator should be a zero degree polynomial, or a constant term, assumed as
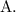
Since
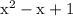 is a second degree polynomial, the numerator of the fraction having this term as denominator should be a first degree polynomial, assumed as
is a second degree polynomial, the numerator of the fraction having this term as denominator should be a first degree polynomial, assumed as
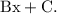
So let,
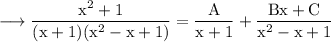
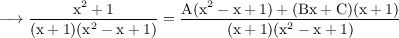
Equating numerators,

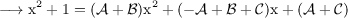
Equating corresponding coefficients,
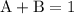
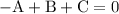
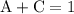
Solving these three equations we get,
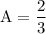
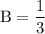
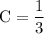
Thus,
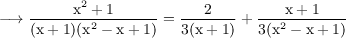
![\small\text{$\longrightarrow\rm{(x^2+1)/((x+1)(x^2-x+1))=(1)/(3)\left[(2)/(x+1)+(x+1)/(x^2-x+1)\right]}$}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/s3hkl9i0kirsqtr3pqpu.png)
So (1) becomes,
![\longrightarrow\underline{\underline{\bf{(x^2+1)/(x^3+1)=(1)/(3)\left[(2)/(x+1)+(x+1)/(x^2-x+1)\right]}}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/pn60gessx7zn4dxtq0xo.png)
Hence the given fraction is resolved into partial fractions.