Question

NO LINKS!! URGENT HELP PLEASE!!

Please help me with 1aa and 2aa

Answer 1

1.23.38 km^2

2.402.84 mi^2

Explanation:

Note:
The area of a polygon can be found using the following formula:

`\boxed{\bold{Area = (Perimeter*apothem)/(2)}}`

where:

Perimeter is the total length of all the sides of the polygon

Apothem is the distance from the center of the polygon to a point on any side

To find , use this formula

`\boxed{\bold{Apothem = ( length\:of\:side )/( 2 *tan((180)/(n)))}}`

where:

n is the number of sides of the polygon

For question:

1.

Perimeter(p)=18km

no. of side (n)=6

length of one side=
`(p)/(n)=(18)/(6)=3` km

Now finding apothem(a),

by substituting value, we get,

`Apothem = ( 3 )/( 2 *tan((180)/(6)))\\Apothem = ( 3 )/( 2 *tan(30))\\Apothem = ( 3 )/( 2 * (√(3))/(3))}\\Apothem =(3√(3))/(2)} \: or\: 2.598km\\`

Now, we have

`A=(1)/(2)*a*P`

substituting value:

`A=(1)/(2)*2.598*18=23.38 km^2`

2.

no. of side (n)=12

length of one side(l)=6 mi

Perimeter(p)=n*l=12*6=72 mii

Now finding apothem(a),

by substituting value, we get,

`Apothem = ( 6)/( 2 *tan((180)/(12)))\\Apothem = ( 6 )/( 2 *tan(15))\\Apothem = ( 3 )/( 2*0.27)}\\Apothem =(6)/(0.54)=11.19mi`

Now, we have

`A=(1)/(2)*a*P`

substituting value:

`A=(1)/(2)*11.19*72=402.84 mi^2`

Answer 2

1) 23.4 km²

2) 403.1 mi²

Explanation:

The formula for the area of a regular polygon is half the product of its apothem and perimeter.

`\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=(1)/(2)aP$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the apothem.\\ \phantom{ww}$\bullet$ $P$ is the perimeter.\\\end{minipage}}`

From inspection of the given regular polygons, we have been given the perimeter or side length only. Therefore, we need to calculate the apothem.

The formula for the length of the apothem of a regular polygon is:

`\boxed{\begin{minipage}{5.5cm}\underline{Length of apothem}\\\\$a=(s)/(2 \tan\left((180^(\circ))/(n)\right))$\\\\where:\\\phantom{ww}$\bullet$ $s$ is the side length.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}`

Question 1

The given polygon has 6 sides, and its perimeter is 18 km. Therefore:

• n = 6
• s = 18/6 = 3 km

Substitute the values of s and n into the apothem formula and solve for a:

`\begin{aligned}\implies a&=(3)/(2 \tan\left((180^(\circ))/(6)\right))\\\\&=(3)/(2 \tan\left(30^(\circ)\right))\\\\&=(3)/(\left((2√(3))/(3)\right))\\\\&=(3√(3))/(2)\end{aligned}`

To find the area of the polygon, substitute the found value of a, along with the perimeter, P = 18, into the area formula:

`\begin{aligned}\implies A&=(1)/(2) \cdot(3√(3))/(2)\cdot 18\\\\&=(54√(3))/(4) \\\\&=23.382685...\\\\&=23.4\; \sf km^2\;(nearest\;tenth)\end{aligned}`

Therefore, the area of the regular polygon is 23.4 km² to the nearest tenth.

`\hrulefill`

Question 2

The given polygon has 12 sides, and the length of one side is 6 miles. Therefore:

• n = 12
• s = 6 miles

Substitute the values of s and n into the apothem formula and solve for a:

`\begin{aligned}\implies a&=(6)/(2 \tan\left((180^(\circ))/(12)\right))\\\\&=(6)/(2 \tan\left(15^(\circ)\right))\\\\&=(3)/(\tan\left(15^(\circ)\right))\\\\&=(3)/(2-√(3))\\\\&=6+3√(3)\end{aligned}`

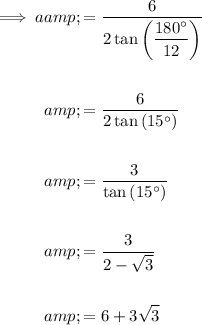
The perimeter of the polygon is n · 2 = 12 · 6 = 72 miles.

To find the area of the polygon, substitute the found value of a, along with the perimeter, P = 72, into the area formula:

`\begin{aligned}\implies A&=(1)/(2) \cdot (6+3√(3))\cdot 72\\\\&=36 (6+3√(3))\\\\&=216+108√(3)\\\\&=403.061487...\\\\&=403.1\; \sf mi^2\;(nearest\;tenth)\end{aligned}`

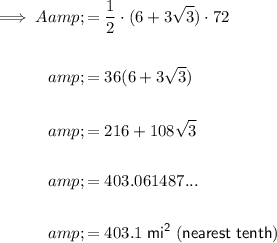
Therefore, the area of the regular polygon is 403.1 mi² to the nearest tenth.