Question

Solve this simultaneous equation
3x-3y=3
x+y=13

Answer 1

Hello !

Answer:

`\Large \boxed{\begin{cases}x=7 \\y=6\end{cases}}`

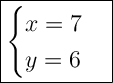
Explanation:

We want to find the values of x and y that satisfy the following system of equations :

`\begin{cases}\sf 3x-3y=3 \\\sf x+y=13\end{cases}`

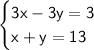
First, let's divide both sides of the first equation by 3 :

`\begin{cases}\sf(1)/(3)(3x-3y)=(3)/(3) \\\sf x+y=13\end{cases}`

`\begin{cases}\sf x-y=1 \ \ \ \ (*)\\\sf x+y=13\end{cases}`

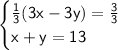
Now let's add the two equations and combine like terms :

`\sf x-y+(x+y)=1+13\\2x=14`

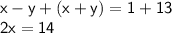
Let's divide both sides by 2 :

`\sf(2x)/(2) =(14)/(2) \\\boxed{\sf x=7}`

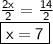
The value of x is now known .

Let's substitute 7 for x in the first equation :

`\sf 7-y=1`

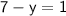
Substract 7 from both sides :

`\sf 7-y-7=1-7\\-y=-6`

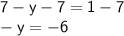
Finally, let's multiply both sides by -1 :

`\sf-1(-y)=-1(-6)\\\boxed{\sf y=6}`

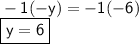
Have a nice day ;)