Question

A hunter walks 400 up a hill which slopes at an angle of 20degree to the horizontal. Calculate correct to the nearest meter;the (a) horizontal distance covered (b)vertical height through which he rises

Answer 1

horizontal distance = 376 meters

vertical height = 137 meters

Explanation:

We can visualize the vertical height(v), horizontal distance (h) and the distance on the hill (400 m) as a right triangle with the angle 20° being the angle between the hill slope and the horizontal distance

The angle between the vertical and horizontal distances is a right angle 90°

The other angle between the vertical distance and the hill slope = 90 - 20 = 70°

By the law of sines

`(h)/(\sin 70) = (v)/(\sin 20) = (400)/(\sin 90)\\\\\\\text{Since $\sin 90 = 1 $ the above relation becomes:}\\\\(h)/(\sin 70) = (v)/(\sin 20) = 400\\\\`

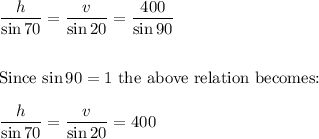
Breaking this into two parts we get

`(h)/(\sin 70) = 400\\\\h = 400 (\sin 70) = 375.87704\dots\;meters\\\\\text{and }\\\\(v)/(\sin 20) = 400\\\\v = 400(\sin 20) = 136.80805 \dots \;meters`

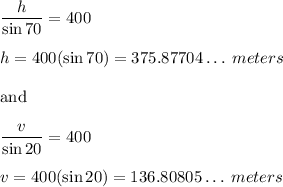
Rounding to the nearest meter we get

horizontal distance = 376 meters

vertical height = 137 meters