Question

A person is turning a wheel to roll up a cord. The wheel has a radius of 40 centimeters and is spinning at 5 revolutions per minute. How much time is needed to wind up 10 meters of cord?​

Answer 1

Approximately
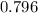`0.796` minutes.

Step-by-step explanation:

Apply unit conversion and ensure that all distances are measured in standard units:

`r = 40\; {\rm cm} = 0.40\; {\rm m}`.

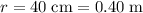The circumference of this wheel is:

`2\, \pi\, r = 2\, \pi\, (0.40\; {\rm m}) = 0.80\, \pi\; {\rm m}`.

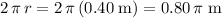Thus, each revolution of the wheel would wind up
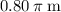`0.80\, \pi\; {\rm m}` of cord.

Multiply the distance winded up per revolution by the rate of revolution to find the rate at which the cord is winded up:

`\begin{aligned} & \frac{0.80\,\pi\; \text{meter}}{1\; \text{revolution}} \cdot \frac{5\; \text{revolution}}{1\; \text{minute}} = \frac{4\, \pi\; \text{meter}}{1\; \text{minute}}\end{aligned}`.

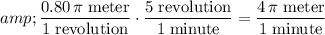Divide the length of the cord by this rate to find the time it takes to wind up the cord:

`\begin{aligned}& \frac{10\; \text{meter}}{4\, \pi\; \text{meter}\cdot \text{minute}^(-1)} \\ =\; & (2.5)/(\pi)\; \text{minute} \\ \approx\; & 0.796\; \text{minute}\end{aligned}`.