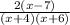Answer:
A.)
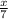
B.)
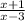
C.)
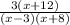 =
=
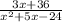
D.)
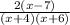 =
=
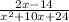
Explanation:
A.)
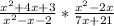 , Firstly you have to factor the denominator (bottom terms on lower part of the fraction.)
, Firstly you have to factor the denominator (bottom terms on lower part of the fraction.)
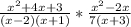 + also make sure that the denominator
+ also make sure that the denominator
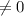 if it's asking for domain, now we do the same for the numerator.
if it's asking for domain, now we do the same for the numerator.
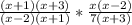 , now we cross-multiply. Get rid of the common factors you see.
, now we cross-multiply. Get rid of the common factors you see.
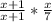 , then simplify further
, then simplify further
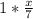 =
=
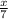
B.) Remember to KCF, keep the first fraction, turn division sign into multiplication, flip second fraction
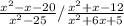 ,
,
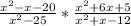 , now do the steps i did in step a.
, now do the steps i did in step a.
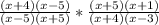 , simplify by cross-multiplying equals to
, simplify by cross-multiplying equals to
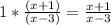
C.)
 , multiply to get same factors for denominator on both sides then add and then simplify.
, multiply to get same factors for denominator on both sides then add and then simplify.
 , for 2nd fraction multiply by x+8,
, for 2nd fraction multiply by x+8,
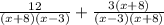 =
=
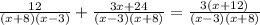
D.) Same as c, just multiply to get same denominator but for both

finally =