Question

Please help me with this

Answer 1

t = 14.9 years

Explanation:

In the given formula for compound interest,

• A is the amount in the account,
• P is the principal (investment),
• r is the interest rate (percentage converted to decimal),
• n is the number of compounding periods per year,
• and t is the time in years.

Step 1: We can start by identifying A, P, r, n, and t:

• A is $10500
• P is $5000
• r is 0.05,
• n is 12 (there are 12 months in a year and since compound interest is yearly, money compounded monthly means there are 12 compound periods),
• and t is unknown

Thus, we plug in 10500 for A, 5000 for P, 0.05 for r, and 12 for n to solve for t, the time it takes for the money to reach $10500:

Step 2: Plug everything in and simplify:

`10500=5000(1+0.05/12)^(^1^2^t^)\\10500=5000(241/240)^(^1^2^t^)`

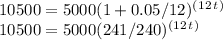
Step 3: Divide both sides by 5000:

`(10500=5000(241/240)^(^1^2^t^))/5000\\2.1=(241/240)^(^1^2^t^)`

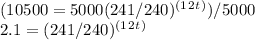
Step 4: Take the log of both sides:

`log(2.1)=log(241/240^(^1^2^t^))`

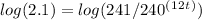
Step 5: Bring down 12t on right-hand side of equation:

`log(2.1)=12t*log(241/240)`

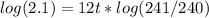
Step 6: Divide both sides by log(241/240):

`(log(2.1)=12t*log(241/240))/log(241/240)\\log(2.1)/log(241/240)=12t`

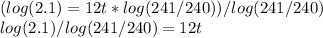
Step 7: Multiply both sides by 1/12 (same as dividing both sides by 12) and round to solve for t:

`1/12(log(2.1)/log(241/240)=12t)\\1/12(log(2.1)/log(241/240))=t\\14.86963953=t\\14.9=t`

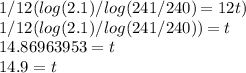
Thus, it will take about 14.9 years for $5000 invested at a bank that pays 5% interest compounded monthly to reach 105000.

Optional Step 8: Check validity of answer by plugging in 14.9 for t in compounded interest formula:

`10500=5000(1+0.05/12)^(^1^2^*^1^4^.^9^)\\10500=5000(241/240)^1^7^8^.^8\\2.1=(241/240)^1^7^8^.^8\\2.1 < 2.103`

Our answer is slightly bigger since 14.9 is rounded to the nearest tenth and it an approximation. However, we can trust our approximation since the answer is close enough.