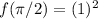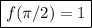Question

Find exact value trigonometry

Answer 1

`f(\pi / 2) = 1`

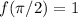
Explanation:

To find the exact output of a function f(x) = sin²x given the input π/2, we can look to the unit circle. Remember that sin²x is an abbreviation for (sin(x))².

We can represent the output of the function for the input π/2 as:

`f(\pi / 2) = (\sin(\pi / 2))^2`

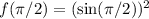
First, we need to find the exact value of sin(π/2). We can find this by graphing
`\theta = \pi/2`, finding its intersection with the circumference of the unit circle, then taking the y-coordinate of the point of intersection.

This y-coordinate is 1.

Therefore,

`f(\pi / 2) = (1)^2`

`\boxed{f(\pi / 2) = 1}`