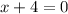Question

F(x) = 3x³ +21x² + 36x.

solve algebraically

Answer 1

`x=0, \: -3, \: -4`

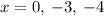
Explanation:

We can solve for the zeros of the function by factoring, then setting f(x) to 0 and solving for x.

First, we can factor out an x.

`f(x) = 3x^3+21x^2+36x`

`f(x) = x(3x^2+21x+36)`

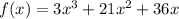
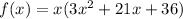
We are left with a quadratic, from which we can factor out a 3.

`f(x) = 3x(x^2+7x+12)`

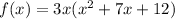
Next, we can factor the quadratic using the rule:

★
`\text{if } x^2 + cx + d = (x + a)(x+b) \text{, then } a+ b = c \text{ and } a \cdot b = d` ★

`f(x) = 3x(x + 3)(x + 4)`

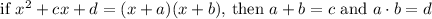The equation is now in a fully factored form. Therefore, we can find the zeros of the function by setting f(x) (the function's output) to 0 and solving for when each factor is equal to 0.

★
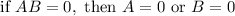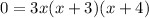
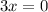
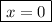
`\text{if } AB = 0, \text{ then } A=0 \text{ or } B=0` ★

`0 = 3x(x + 3)(x + 4)`

`3x = 0`

`\boxed{x = 0}`

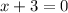
OR

`x+3=0`

`\boxed{x = -3}`

OR

`x+4 = 0`

`\boxed{x = -4}`