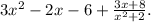The quotient of the expression is
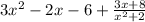 . Hence, option (a) is correct.
. Hence, option (a) is correct.
Step 1: Set up the long division.
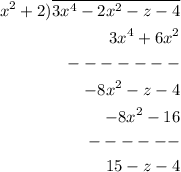
Step 2: Divide the first term of the dividend by the first term of the divisor.
The leading term of the dividend is
 , and the leading term of the divisor is
, and the leading term of the divisor is
 . Dividing
. Dividing
 by
by
 , gives 3x
, gives 3x
Step 3: Multiply the divisor by the quotient.
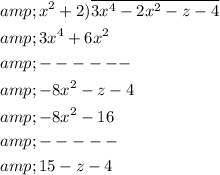
Step 4: Subtract the product from the dividend.
Subtracting
 from
from
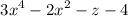 gives
gives
 .
.
Step 5: Bring down the next term of the dividend.
The next term of the dividend is -z-4.
Step 6: Repeat steps 2-5 until the remainder is either zero or a polynomial of lower degree than the divisor.
Dividing
 by
by
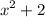 gives
gives
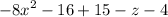 . Since the remainder is 15-z-4, which is a polynomial of lower degree than the divisor, the division is complete.
. Since the remainder is 15-z-4, which is a polynomial of lower degree than the divisor, the division is complete.
Step 7: Write the quotient and remainder.
The quotient is
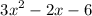 , and the remainder is 15-z-4. Therefore, the final answer is
, and the remainder is 15-z-4. Therefore, the final answer is