Question

A triangle has a perimeter of 280 cm, and its side lengths are a, b and c respectively. If

a:b= 2:3, b:c=4:5, find the length of each side of the triangle.​

Answer 1

The length of the sides are 64 cm, 96 cm and 120 cm.

Explanation:

Perimeter of a triangle:

The perimeter of a triangle is the sum of it's sides.

A triangle has a perimeter of 280 cm, and its side lengths are a, b and c respectively.

This means that:

`a + b + c = 280`

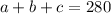
a:b= 2:3

This means that:

`(a)/(b) = (2)/(3)`

`2b = 3a`

`b = (3a)/(2)`

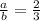
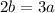
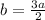
b:c=4:5

This means that:

`(b)/(c) = (4)/(5)`

`4c = 5b`

`c = (5b)/(4)`

`c = (5*3*a)/(4*2) = (15a)/(8)`

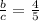
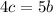
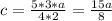
At the original equation:

We replace b and c in function of a. So

`a + b + c = 280`

`a + (3a)/(2) + (15a)/(8) = 280`

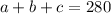
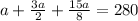
Multiplying everything by 8

`8a + 12a + 15a = 280*8`

`35a = 280*8`

`a = (280*8)/(35)`

`a = 64`

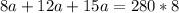
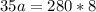
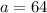
Sides b and c:

Since we have a, we can find sides b and c:

`b = (3a)/(2) = (3*64)/(2) = 3*32 = 96`

`c = (15a)/(8) = (15*64)/(8) = 15*8 = 120`

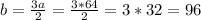
The length of the sides are 64 cm, 96 cm and 120 cm.