Answer:
x = 8
Explanation:
To find the value of x, we can use the Intersecting Secants Theorem.
The Intersecting Secants Theorem states that the product of the measures of one secant segment and its external part is equal to the product of the measures of the other secant segment and its external part.
The given diagram shows two secant segments TR and QR that intersect at exterior point R. Their external parts are SR and PR, respectively.
Therefore, according to the Intersecting Secants Theorem:

Given values:
- TR = x + 10
- SR = 10
- QR = 11 + 9 = 20
- PR = 9
Substitute the values into the equation and solve for x:
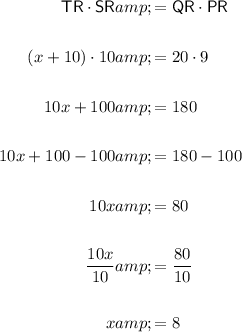
Therefore, the value of x is 8.