Question

Car 1 travels 8 miles north and then 6 miles east. Car 2 travels 12 miles south and 9 miles west. Distance in miles between the cars

Answer 1

`\text{Distance in miles between the cars = 25 miles}`

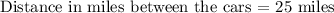
Explanation:

We can solve this problem by treating the locations of the cars as points on a X-Y coordinate plane

Let the X axis represent the horizontal distances with direction East being positive and direction West being negative

Let Y represent the vertical distance with North being positive and South being negative

The initial position of both cars is (0, 0)

Car 1 travels 8 miles north so it's y coordinate becomes 0 + 8 = 8 and point coordinates become (0, 8)
It then travels 6 miles east which puts its x-coordinate at 0 + 6 = 6 with y-coordinate staying at 8
So position of car 1 is (6, 8)

Car 2 travels 12 miles south first so new y-coordinate = 0- 12 = -12
It then travels 9 miles west so new x-coordinate = 0 - 9 = -9

Position of car 2 is (-9, -12)

The distance between these two points, d is the distance between the cars

The distance between any two points (x1, y1) and (x2, y2) is given by the distance formula

`d = \sqrt {(x_(2) - x_(1))^2 + (y_(2) - y_(1))^2}`

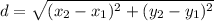
If we let (x1, y1) represent the position of car 2 and (x2, y2) the position of car 1 then

`d = \sqrt {(6 - (-9))^2 + (8 - (-12))^2}\\\\d = \sqrt {(15)^2 + (20)^2}\\\\d = \sqrt {{225} + {400}}\\\\d = \sqrt {625}\\\\d = 25`

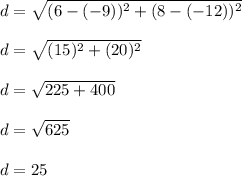
So the distance between the two cars = 25 miles

See attached image for a visual rendering