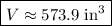Question

A right rectangular prism measures 8 inches long, 12 inches high, and 6 inches deep. A half-sphere with a diameter of 2 inches is carved out of the prism. What is the approximate volume of the resulting composite figure?

Answer 1

`573.9 \text{ in}^3`

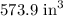
Explanation:

First, we can find the volume of the rectangular prism using the formula:

`V_\square = l \cdot w \cdot d`

where
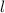`l` is the prism's length,
`w` is its width, and
`d` is its depth.

Plugging the given dimensions into the formula:

`V_\square = 8 \cdot 12 \cdot 6`

`V _\square= 96 \cdot 6`

`\boxed{V_\square = 576 \text{ in}^3}`

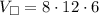
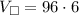
Next, we can find the volume of the half-sphere using the formula:

`V_\circ = (2)/(3) \pi r^3`

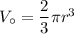
where
`r` (or
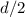`d/2`) is the half-sphere's radius.

Plugging the given diameter value into the formula:

`V_\circ = (2)/(3) \pi (2/2)^3`

`V_\circ = (2)/(3) \pi (1)^3`

`\boxed{V_\circ=(2)/(3)\pi \text{ in}^3}`

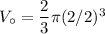
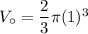
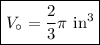
Finally, we can find the volume of the composite figure by subtracting the volume of the half-sphere from the volume of the rectangular prism.

`V = V_\square - V_\circ`

`V = 576 \text{ in}^3 - (2)/(3)\pi \text{ in}^3`

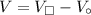
We can evaluate this using a calculator.

`\boxed{V\approx 573.9 \text{ in}^3}`