Question

A car can go from 0 to 91 km/hr in 6 seconds. What would be its final speed after 9 seconds if its starting speed

was 37 km/hr? (round to nearest whole number)

Answer 1

The final speed after 9 seconds would be approximately 118 km/h.

What is uniform rectilinear motion?

It is a type of motion in a straight line in which the speed of an object is constantly changing due to constant acceleration. Acceleration can be positive or negative, which determines whether the object is speeding up or slowing down. This concept is fundamental to understanding how objects move and change speed in real situations.

To solve this problem, we first need to convert the given velocities to meters per second (m/s), since acceleration will be given in units of m/s².

The initial speed is: 37 km/h, we pass it to m/s, then
`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_o=37 \ \frac{\\ot{km}}{\\ot{h}}*\left(\frac{1000 \ m}{1\\ot{km}}\right)*\left(\frac{1\\ot{hr}}{3600 \ s}\right)\approx10.28 \ m/s } \end{gathered}$} }`

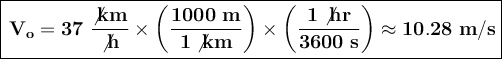
The final speed that is reached is 91 km/h, remembering that this is not the value that we are asked to calculate.
`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_f=91 \ \frac{\\ot{km}}{\\ot{h}}*\left(\frac{1000 \ m}{1\\ot{km}}\right)*\left(\frac{1\\ot{hr}}{3600 \ s}\right)\approx25.28 \ m/s } \end{gathered}$} }`

Acceleration is calculated using the average acceleration formula:
`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{a=(V_f-V_o)/(t) } \end{gathered}$} }`

Where:

• a is the acceleration
• Vf is the final speed
• Vo is the initial velocity
• t is the time

Substituting the known values, we get:
`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{a=(25.28 \ m/s-10.28 \ m/s)/(6 \ s) } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{a\approx2.5 \ m/s^2 } \end{gathered}$} }`

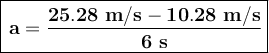
Now, we can use acceleration and time to calculate the final velocity after 9 seconds using the following formula:

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_f=V_o+a* t } \end{gathered}$} }`

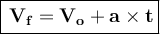
Where:

• a is the acceleration
• Vf is the final speed
• Vo is the initial velocity
• t is the time

Substituting the known values, we get:
`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_f=10.28 \ (m)/(s)+2.5 \ \frac{m}{\\ot{s^2}}* 9 \ s } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_f=10.28 \ (m)/(s)+22.5 \ (m)/(s) } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_f\approx33.78 \ m/s} \end{gathered}$} }`

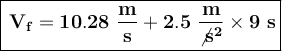
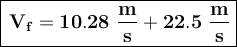
Finally, we convert the final speed to km/h:
`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_f=32.78 \ \frac{\\ot{m}}{\\ot{s}}*\left(\frac{1 \ km}{1000\\ot{m}}\right)*\left(\frac{3600\\ot{s}}{1 \ h}\right) } \end{gathered}$} }`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{V_f\approx118 \ km/h } \end{gathered}$} }`

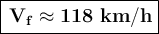
The final speed after 9 seconds would be approximately 118 km/h.