Question

Find the 9th term of the geometric sequence 8,32,128,...

Answer 1

9th term = 524288

Explanation:

An equation we can use to find the nth term in a geometric sequence is:

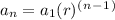`a_(n)=a_(1)(r)^(^n^-^1^)`, where

• a1 is the first term,
• r is the common ratio (i.e., dividing successive terms always returns the common ratio),
• and n is the term position (e..g, first, third, etc.)

Step 1: We're already given that a1 = 8 and that n = 9 (since we want to find the 9th term). However, we need to find the common ratio by dividing two consecutive terms with the successive term being divided by the preceding term. We can divide 32 by 8 to find r, the common ratio:

r = 32/8

r = 4

Thus, the common ratio of the sequence is 4

Step 2: In order to find the 9th term of the sequence, we can plug in 8 for a1, 4 for r, and 9 for n and simplify:

`a_(n)=8(4)^(^9^-^1^)\\a_(n)=8(4)^8\\a_(n)=8(65536) \\a_(n)=524288`

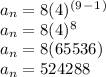
Thus, the 9th term of the geometric sequence is 524288.