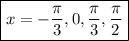Question

Find all Solutions of the equation

Answer 1

`\textsf{D)} \quad x=-(\pi)/(3), 0, (\pi)/(3), (\pi)/(2)`

Explanation:

To find the solutions of the given trigonometric equation, begin by factoring out the common term sin 2x:

`\begin{aligned}2 \sin 2x \cos x - \sin 2x & = 0\\\sin 2x(2 \cos x - 1)&=0\end{aligned}`

Set each factor equal to zero and solve for x using the unit circle.

`\begin{aligned}\sin 2x & = 0\\2x & = \sin^(-1)(0)\\2x&=0+ 2\pi n, \pi + 2 \pi n\\ x&=\pi n, (\pi)/(2)+\pi n \end{aligned}`

`\begin{aligned}2\cos x - 1 & = 0\\2 \cos x& = 1\\\cos x&=(1)/(2)\\x&=\cos^(-1)\left((1)/(2)\right)\\x&=(\pi)/(3)+2\pi n, (5\pi)/(3)+2 \pi n\end{aligned}`

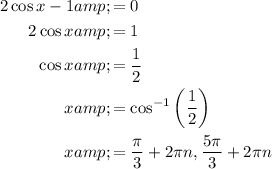
Therefore, the solutions in the given interval -π/2 < x ≤ π/2 are:

`\boxed{x=-(\pi)/(3), 0, (\pi)/(3), (\pi)/(2)}`