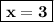Answer:
x = 3
y = -1
Explanation:
Solving system of equations:
Method: substitution
x - 3y = 6 --------------(I)
x = 6 + 3y -------------(II)
2x + 2y = 4 ----------(III)
Substitute x = 6 +3y in equation (II),
2*(6+3y) + 2y = 4
Use distributive property to open the parenthesis,
2*6 + 2*3y + 2y = 4
12 + 6y + 2y = 4
Combine like terms.
12 + 8y = 4
Subtract 12 from both sides,
8y = 4 - 12
8y = -8
Divide both sides by 8,
y = -8÷ 8
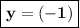
Substitute y = -1 in equation (II) and find the value of x.
x = 6 + 3*(-1)
= 6 - 3