Question

How long will it take for an investment to triple, if interest is compounded continuously at 5%?

It will take (blank) years before the investment triples.

Answer 1

It will take 22 years before the investment triples.

Explanation:

To determine how many years it will take for an investment to triple if interest if compounded continuously at 5%, use the continuous compounding interest formula.

`\boxed{\begin{minipage}{8.5 cm}\underline{Continuous Compounding Interest Formula}\\\\$ A=Pe^(rt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\\phantom{ww}$\bullet$ $P =$ principal amount \\\phantom{ww}$\bullet$ $e =$ Euler's number (constant) \\\phantom{ww}$\bullet$ $r =$ annual interest rate (in decimal form) \\\phantom{ww}$\bullet$ $t =$ time (in years) \\\end{minipage}}`

Given values:

• A = 3P (triple the principal amount)
• P = P
• r = 5% = 0.05

Substitute the given values into the formula and solve for t.

`\implies 3P=Pe^(0.05t)`

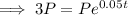
Divide both sides of the equation by P:

`\implies 3=e^(0.05t)`

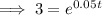
Take natural logs of both sides of the equation:

`\implies \ln 3=\ln e^(0.05t)`

`\textsf{Apply the log power law:} \quad \ln x^n=n \ln x`

`\implies \ln 3=0.05t\:\ln e`

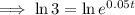
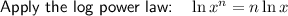
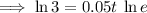
As ln e = 1, then:

`\implies \ln 3=0.05t`

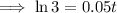
Divide both sides of the equation by 0.05:

`\implies (\ln 3)/(0.05)=t`

`\implies t=20\ln3`

`\implies t=21.9722457...`

`\implies t=22\;\sf years\;(nearest\;year)`

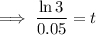
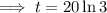
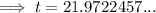
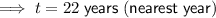
Therefore, it will take 22 years before the investment triples.