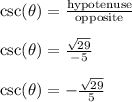Question

Given tan theta = -5/2
and cos theta =2/√29
find csc theta:

Answer 1

Answer:
`-(√(29))/(5)\\\\`

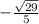
This is the same as writing -sqrt(29)/5

====================================================

Step-by-step explanation:

tan(theta) < 0 and cos(theta) > 0 indicates angle theta is in quadrant IV.

In this quadrant, csc(theta) is negative.

The diagram is shown in the image below. We have these three sides

• opposite = -5
• adjacent = 2
• hypotenuse =
  `√(29)`

Cosecant is the ratio of hypotenuse over opposite. It is the reciprocal of sine.

`\csc(\theta) = \frac{\text{hypotenuse}}{\text{opposite}}\\\\\csc(\theta) = (√(29))/(-5)\\\\\csc(\theta) = -(√(29))/(5)\\\\`